Brain-wide correspondence ofgenomics and projections
by admin
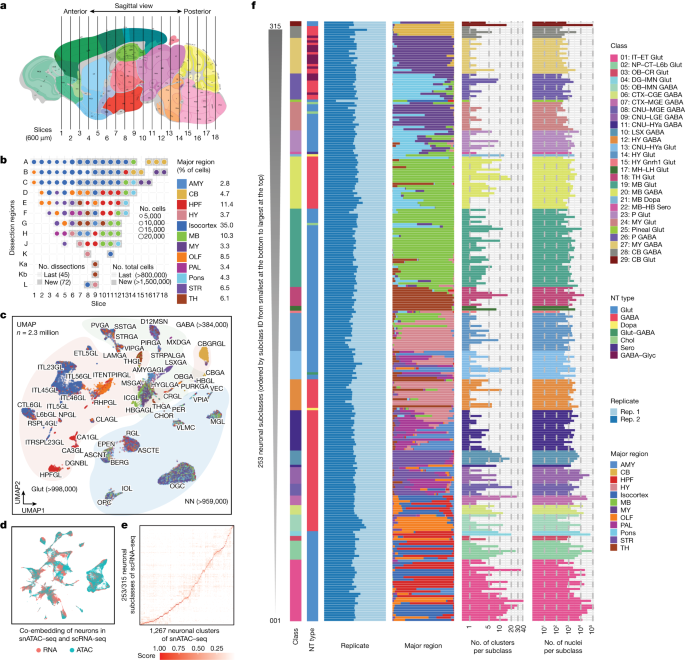
Clustering and interaction of single nuclei in hg19, mm10, and the mouse nucleus ChromHMM38 states for mouse brain
No statistical methods were used to determine sample sizes. There was no randomization of the samples, and investigators were not blinded to the specimens being investigated. However, clustering of single nuclei based on chromatin accessibility was performed in an unbiased manner, and cell types were assigned after clustering. Low-quality nuclei and potential barcode collisions were excluded from downstream analysis as described above.
External datasets used were as follows: (1) ENCODE rDHS regions for both hg19 and mm10 are obtained from SCREEN database (https://screen.encodeproject.org)39,40. (2) ChromHMM38,102 states for mouse brain are download from GitHub (https://github.com/gireeshkbogu/chromatin_states_chromHMM_mm9) and coordinates are LiftOver (https://genome.ucsc.edu/cgi-bin/hgLiftOver) to mm10 with the default parameters96. The UCSC Genome Browser contains a section containing the conserved elements of phastcons 103. The blacklist file was downloaded from the web site www.mitra.stanford.edu. There is genome information for the mouse on the GENCODE (www.gencodegenes.org).
To evaluate the confidence of identified subclass-specific cCRE–gene pairs, we randomly selected 11 major subclasses. We found that there is statistically significant higher enrichment (P = 0.004) of chromatin interaction signal at the corresponding subclass-specific cCRE–gene pair anchors, compared with non-corresponding pair anchors (Extended Data Fig. 10g), suggesting that subclass-specific cCRE–gene pairs are more likely to interact in the cell types in which the cCREs are active.
Modeling cCREs in the mouse brain with CellOracle52 & gimmemotifs83: a subclass-level deep learning approach
We trained the subclass-level deep-learning model on four NVIDIA A100 80 GB GPUs using the script basenji_train.py from Basenji65. For training, we set the parameter batch size to 32, epochs to 150 and patience to 30.
The i represent the cell type, and j represents genomic bins. The ytrue is a matrix of genes calculated from signals. The bin-by-type matrix is represented by the ypred. The pairwise covariance wi,i was calculated between cell types. We then sum the scores across rows and normalize the number of cell types as weights. The weights were dot multiplication by the original poisson loss.
The model architecture, layers and parameters are adapted from the mouse model from a previous study80, with modification only in the last output head layer with parameter: “units”: 275. One novel loss function was developed to encourage the model to predict cCREs in under represented cell types.
We adapted the recently published Python package CellOracle52 on our data to infer GRNs for each cell subclass across the whole mouse brain based on our integration analysis between our snATAC–seq data and the scRNA-seq data5. Three steps were followed. First, we identified the co-accessibility distal-to-proximal pairs, which was described previously for each subclass. Second, we mapped the distal cCREs to TFs. Lastly, we identified the regulatory relationships between TFs and the potential target genes by fitting a regularized linear regression model using scRNA-seq data. The second step is what we used for the Python package gimmemotifs83, which is the default motifs database provided by CellOracle. The genes that the cCREs were mapped to were based on GENCODEmm10, the same as above. The samples were random and all of the cells from every subclass were used if there was more than 1,000 cells. The find variable features function of Seurat was used to find the top genes, and then manually add the 499 TFs that were missed in the previous 3,000 genes. 5. For each subclass, we performed CellOracle on the scRNA-seq data with the default parameters. We used P < 0.001 and the top 10,000 edges based on the absolute values of the weights to filter the predicted interactions between TFs and genes as suggested by CellOracle. Finally, 267 out of 275 subclasses successfully had the predicted GRNs.
We performed GO enrichment analysis using R package clusterProfiler100,101. The background genes were selected on the basis of the enrichment analysis and described in text. The P value was computed using the Fisher exact test and adjusted for multiple comparisons using the Benjamini–Hochberg method.
To analyse the TE-accessible variability with decreased noise, the TE signal was aggregated from the TE-cCREs. We averaged and normalized theTE-cCRE to get the correlation between the two. The companion paper41 contained a signal for eachTE in matched subclasses. The correlation between accessibility and expression was calculated using the aggregated signals from a previous study.
The TE annotation of cCREs was annotated using Homer45 and UCSC mm10 refGene and RepeatMasker annotation. To define the high TE-cCREs fraction of subclasses, we fitted a mixture model for the TE-cCRE fraction across all subclasses using the R package mixtools97 (v.2.0.0). The null distribution was used to calculate the P value.
We chose two peak modules that show global accessibility across the subclasses based on the NMF analysis. We then selected all of the proximal–distal connections with cCREs in the peak modules above and ranked the proximal–distal connections based on the highest Cicero scores they have. We treated them as global proximal–distal connections and performed the Hi-C signals by aggregating all of the Hi-C data. From the heat maps (Extended Data Fig. 10h), we observed the strong enrichment signals for the global proximal–distal connections.
Permutation analysis of frequently interacting regions in the mouse cortex 38: Identifying the relative accessibility of cCREs and their overlaps at FIREs
CCREs are enriched at FIREs, but we tested that through permutation analysis. In brief, we shuffled the mouse genome 1,000 times, each time generating 1,053,811 random regions with equivalent sizes as the cCREs. We then calculated the number of overlaps between the randomly generated regions and the FIREs during each shuffle. We found that cCREs are significantly enriched at FIREs (P < 0.001; Extended Data Fig. 10f), with the actual number of overlaps on FIREs substantially higher than expected.
We called frequently interacting regions (FIREs) in the mouse cortex38 by applying the criteria in our group’s FIRE paper95. The result showed that a lot of FIREs and cCREs are indistinguishable in the mouse brain.
The basis matrix was used to connect each module with accessible elements. For each element and each module, we derived a basis coefficient score, which represents the accessible signal contributed by all clusters in the defined module. We calculated a score called feature score for each accessibility element using the kim method. The feature score ranges from 0 to 1. A high feature score means that a distinct element is specifically associated with a specific module. The features that fulfilled both of the criteria were retained as module specific elements.
The relative accessibility of cCREs was the basis for grouping them into cis-regulatory modules. We adapted NMF (Python package sklearn90) to decompose the cell-by-cCRE matrix V (N × M, N rows: cCRE, M columns: cell clusters) into a coefficient matrix H (R × M, R rows: number of modules) and a basis matrix W (N × R), with a given rank R19:
Only peaks on chromosomes 1–19 were retained and both sex chromosomes were included in the list of blacklisted regions. A union peak list for the whole dataset was obtained by merging peak sets from all of the cell clusters using BEDtools91.
For every cell cluster above, we combined all properly paired reads to generate a pseudobulk ATAC–seq dataset for individual biological replicates. Half of the reads from each biological replicate were created in two pseudoreplicates. The peaks for each of the datasets were identified by the pool of replicates. Peak calling was performed on the Tn5-corrected single-base insertions using MACS236 with the following parameters: Shift 75, extsize 150, no model, call-summits, SMPR. Finally, we extended peak summits by 250 bp on either side to a final width of 501 bp for merging and downstream analysis. If the number of cells in any of the pseudobulk ATAC–seq is less than 200, we decided not to use MACS2 for it. We used this method to decrease the chance of false negatives during the next part of the process.
To generate a list of reproducible peaks, we retained peaks that (1) were detected in the pooled dataset and overlapped ≥50% of peak length with a peak in both individual replicates or (2) were detected in the pooled dataset and overlapped ≥50% of peak length with a peak in both pseudoreplicates.
We performed peak calling according to the ENCODE ATAC–seq pipeline (https://www.encodeproject.org/atac-seq/) on 1,482 L4-level subtypes and used the same procedure to filter the peaks at both the bulk and single-cell level (Extended Data Fig. 9a) as in our previous study19. If the number of cells less than 200 were shared, we merged the clusters with the number of cells less than 200 in the L 3-level cluster. Next, 1,493 of the various types were used.
We first imputed RNA expression levels according to the chromatin accessibility of the gene promoter (up to 2 kb to TSSs) and gene body as described previously32 using the function make_gene_matrix in SnapATAC2. We used Seurat32 for integration analysis for both neuroscience and fibroblasts. In the scRNA-seq data, we randomly chose 50 cells for each of over 5,000 clusters, and got over 200,000 cells. To have a comparable number of cells in our snATAC–seq data, we randomly selected 150 cells for each of over 1,260 L4-level neuronal subtypes and got over 180,000 nuclei. For non-neuronal cells, we sampled 500 cells per cluster and got 35,000 cells in the scRNA-seq data. For the snATAC–seq, we sampled 300 cells per L4-level subtypes, and got over 57,000 nuclei.
The k-nearest neighbour graph was created by applying the function knn from snapA Tac2 and setting the parameters n_neighbors and kd tree. The function leiden was used to clusters with the object function set as modularity. The parameters that affected the number of clusters a lot was chosen from 0.1 to 2 and the step size was based on the silhouette coefficients. We check the UMAP 81 for each clustering result to make sure that it’s compatible with the top silhouette coefficients. UMAP projections were calculated using the Python package umap with the parameters a as 1.8956, b as 0.8005 and init as spectral. All of the resolution parameters during clustering are provided in Supplementary Table 3. In our later analysis, we used the term subtypes to represent all of the final clusters from L3-level clustering and L4-level clustering.
We applied the function of spectral from SnapATAC2 to convert the high-dimension sparse 500 bp genomic bin features per cell into low dimensional representations, which used spectral embedding of the normalized graph Laplacian defined by the cell-to-cell similarity matrix using cosine distance. 50 as the dimensions of the low-dimensional representation space was used for the L1 level and L2 level clustering to account for a large amount of cells and potentially diverse cell types. The top 50 components were used to rank all of the components, so that we could analyze them. For later analysis, we chose 30 instead. The function function spectral had a true weighted_by_sd parameter. We did not use the parameter ‘sample_size’ in the function spectral, so no approximation method was used for the spectral embedding. For 2.3 million cells, it took about 300 GB memory in our high-performance computing system88.
Simultaneous extraction, sorting, alignment and aggregation of frozen tissue dissectates for TAC-seq enrichment in the mouse brain
Frozen mouse brains were securely mounted by the cerebellum or by the olfactory/frontal cortex region onto cryostat chucks with OCT embedding compound such that the entire anterior or posterior half (depending on dissection targets) was left exposed and thermally unperturbed. The section of anterior–posterior spans were performed with hand in the cryostat, using an eyelid microscalpel and surgical LOUpes. 10 m sections were taken at the anterior dissection junctions and imaged after Nissl staining. There was a 0.25 liter tube used to process each excised tissue dissection. Nuclei were extracted from these frozen tissue dissectates within 2 days using gentle detergent-based dissociation as described below.
Paired-end sequencing reads were demultiplexed and the cell index was transferred to the read name. Sequencing reads were aligned to the mm10 reference genome using bwa84. The fragment length contribution is a characteristic for ATAC–seq libraries. We applied quality control criteria, such as retaining only fragments with a quality score of 30 or more, and removing PCR duplicate, whenever we combined theSequencing reads to fragments. Cell barcodes were used to sort the reads and to correct 9 bp duplication from Tn5 transposase 85 during processing.
The data quality was quantified without the need for a peak set. We followed a previously described procedure86, and used the function filter_cells in SnapATAC2 to calculate TSS enrichment (TSSe). TSS positions were obtained from the GENCODE87 database v.16. In brief, Tn5-corrected insertions were shifted +4 bp and reads were shifted -5 bp and aggregated to the unique TSS genome wide. The profile was normalized to the mean accessibility of 2,900–2,400 bp and smoothed out every 11 bp. The maximum of the smoothed profile was taken as the TSSe.
Nuclei with ≥1,000 uniquely mapped fragments and TSSe ≥ 10 were filtered for each of 234 samples according to the ENCODE ATAC–seq data standards and process pipeline (https://www.encodeproject.org/atac-seq/). We used the filter_cells function of SnapATAC2 to achieve this.
We used different versions of Scrublet to remove doublets for every sample. First, we used the add_tile_matrix function to add the 500 bp genomic bin features, then used the select_features function to filter out the features with frequencies along the samples of lower than 0.5% or higher than 99.5%. We then applied the scrublet function of SnapATAC2 to get the doublet scores. The parameter expected_doublet_rate was set to 0.08, which is based on our previous experiment on the snATAC–seq pipeline19. The barcodes that had scrublet scores greater than 0.5 were looked at as potential doublets.
We compared Scrublet with another recently published method named AMULET30, which is used for doublet detection and removal in snATAC–seq data. We simulated datasets containing singlets and artificial doublets from eight samples in the primary motor area and evaluated the performances of the two methods using precision-recall curve (PRC) and area under PRC (AUPRC).
Candidate ARGs in the neuronal pseudocells from an ensemble database of mC-RNA co-clusters
GRNs were built based on correlations between data things and binding motifs so they capture indirect and false positives. Perturbation experiments would be necessary to validate the connections between cis or trans regulators and target genes.
An ensemble database containing 49,504 motif position weight matrices was collected from 29 sources. The clustering ofundant motifs using TOMTOM45’s calculations was done by the SCENIC+ authors. Each motif cluster was annotated with one or more mouse TF genes. TheCluster-Buster46 implementation in SCENIC+ scanned the motifs in the same cluster with hidden Markov models to calculate their occurrence on the DMR.
The unbiased snmC-seq cells from each mC–RNA co-cluster were merged to generate pseudobulk methylation profiles. The epi-retro-seq cells were not used owing to the different genome backgrounds of the mice to avoid confounding results. DMRs were identified within each region group between clusters using ALLCools. The PCC was calculated between the genes. We shuffled the DMRs and genes within each sample to calculate the null PCC and estimate FDR. FDR was used to exclude the target edges from the filter.
To make our candidate ARGs list, we divided our neuronal pseudocells into 28 cell groups, each with its own excitatory and inhibitory populations, and all other cell types were grouped across all of them. We computed pairswise genes from the R package and put them together to create networks within each cell group. For a gene g to be considered an ARG candidate, its correlation r with Fos must be the following: (1) r is greater than or equal to 0.3; (2) r in the greater than or equal to 99.5% quantile distribution of g’s correlations with all genes; and (3) r is statistically significant after multiple hypothesis testing (Holm-adjusted P < 0.05). To construct the final full ARG candidate list, we took the union of selected genes across all cell groups.
The lack of overlap between the brain regions profiled in the two datasets is the main reason for the weak associations between projection-associated and behavior-associated clusters. Additionally, because there were far fewer cells profiled in epi-retro-seq versus Act-seq, the granularity of clusters used for projection association and behaviour association is different; this difference is particularly pronounced in VMHvl for which >10 times more cells were used for the behaviour-association study (Extended Data Fig. 7c–e). Increasing the size of datasets to achieve higher levels of cell typing in specific regions could lead to further association between certain types with projections and behaviors. Our study focused on targets that did not receive strong input from VmH and what a large number of projections across the whole brain looked like. This apparently limited the data overlap between these and limited the ability to make direct comparisons between studies.
Finally, the neurons from each region group were selected and integrated with the scRNA-seq cells from the same region group, using the same procedure as described above. The mC–RNA co-cluster labels were transferred from the scRNA-seq cell to the MERFISH cells. The MERFISH cells assigned to the MM and DCO subclasses in the last step were also excluded as those clusters were not included in the co-cluster analysis as described in the previous section.
This could also be achieved with the registration of MERFISH DAPI images to the framework. The procedure is complex and it is important to use cell types with known locations in order to refine the registration.
The MERFISH experiments were conducted as described in ref. 17, including the gene panel design, tissue preparation, imaging, data processing and annotation. The dataset has two sceltTAL slices, with S 1 and S2 being more like the outside of the body, and 14 sceltTAL slices, with both being more like the inside of the body. The same naming of slices was used throughout this manuscript (Figs. 3e, 4d and 5c and Extended Data Fig. 6).
We used the absolute proportions and not the relative ones because of the different profiling strategies between the two datasets. We pooled the different dissections from different sources into a single source for FANS so that the percentage of cells from different sources is the same. However, the unbiased snmC-seq profiled all of the dissection regions separately and sequenced the same number of cells in each dissection, which manually amplified the proportion of cells from the smaller or sparser dissection regions relative to the larger or denser ones, and limited the power to estimate the real proportion of neurons in each cluster from the sources.
The cortical cells from the 286 experiments were further sorted to exclude the experiments with high proportion of cells that did not project to the intended injection location, using the same method as in our previous study. Specifically, for each FANS run, we counted the number of neurons that were observed in known on-target cell types (({O}{{\rm{on}}})) and off-target cell types (({O}{{\rm{off}}})). Assuming that the proportions of contaminated cells in each subclass would be similar to those of a sample without projection-type enrichment, we compared the observed counts to the counts from unbiased snmC-seq data (({E}{{\rm{on}}}) and ({E}{{\rm{off}}})) collected from the corresponding dissections in Extended Data Fig. 1. The fold enrichment was computed as (\frac{{O}{{\rm{on}}}{E}{{\rm{off}}}}{{O}{{\rm{off}}}{E}{{\rm{on}}}}). The test was used to determine if the enrichment of on-target cells was significant. The P value was computed as (\Pr (X\ge {O}{{on}}{;n},p)), in which (X \sim {\rm{binomial}}(n,p)), where ~ represents distributed as, (n={O}{{\rm{on}}}+{O}{{\rm{off}}}) and (p=\frac{{E}{{\rm{on}}}}{{E}{{\rm{on}}}+{E}{{\rm{off}}}}). For each ET target, we considered ET as on-target subclasses and IT+inhibitory neurons as off-target. The thresholds for fold enrichment and FDR (Benjamini–Hochberg procedure) were 8 and 0.001. For IT targets, we considered IT as on-target subclasses and layer 6 corticothalamic+inhibitory neurons as off-target. The thresholds were 3 and 0,00 for FDR and fold enrichment. This eliminated 32 out of 286 sorting cases (Extended Data Fig. 2e).
We used a model to find the five nearest snmC- by converting Epi-retro-seq cells to the same space. Reciprocally, we fit another PCA model with the epi-retro-seq cells and transform the snmC-seq cells and find five nearest epi-retro-seq cells for each snmC-seq cell. The scores were identical between the two datasets and used the same method as Seurat v3.
A similar framework was adopted by us to integrate data, by identifying the mutual closest neighbours and then aligning the datasets through them.
Predicting Projections of Neurons based on DNA Methylation: Comparing the Performance of Different Logistic Regression Models
To test the similarity of two groups of cells based on DNA methylation, we trained logistic regression models to predict the group label of each cell. We compared the results using four different types of feature to predict the projection target of neurons from the same source. The level of the gene-body is included in these as are the dimensions of the two matrices. 50 PCs were used to make a cut in the data by using snmC-seq to fit the PCA models. We used two different methods to divide the cells. One used a random selection of half of the cells projecting to each target for training and the other half for testing (computational replicates); the other was based on the sex of the mice from which the cells were collected (biological replicates). After the QC steps, we have 168 source–target combinations with data from both sexes and the other 57 with cells from only one sex. Therefore, all of the comparisons of 926 target pairs could be quantified with the computational replicates, but only 516 of them could be quantified with biological replicates. The model performance between different features and different train/test splits was very similar. 3a–c). The performance when using 100-kb bins was very similar to that when using gene bodies (Extended Data Fig. 3a). The performance when using raw features was slightly better than that when using PCs (Extended Data Fig. 3b). Computational replicates were better than biological replicates in terms of performance. 3c), which was expected given that the computational replicates dismissed the heterogeneity between biological replicates and made the predictions easier. Computational replicates provided strong correlations to biological replicates. The comparison between target pairs could be done to evaluate their differences.
Technical reasons would include the following. First, the contamination levels of some experiments might be relatively high, which make larger noise and hinder the models from capturing real projection differences. Different epigenetic differences between neurons are found across replicates. Third, the sample sizes of some projections are small, which makes learning more challenging. Fourth, the models are not powerful enough to capture the complex differences between projections.
The identity of the neurotransmitter was assigned to each cell type based on the number of genes that are essential for its function. Specifically, we used a non-zero threshold nz = 0.35.
All of the other results were computed using a method called Computational replicates. The features were adjusted based on the read coverage of the cells. The model was created when we removed 100 k bins and genes that were 500 average CH base calls. Sci-kit learn was used for model implementation. To measure the performance of the model, an area under the receiver operating characteristic was used. The better ability of the model to present the group label was shown by the higherAUROC, which indicated that the two groups had larger differences. For computational replicates, we carried out random sampling 50 times with different seeds, and used the average AUROC as the final result.
Towards a Brain-Wide Correspondence between Neuronal Epigenomics and Distant Projections. Part I: Cell Type Classification
A without labels and B without labels are both in a co-embedding space. In order to find the nearest neighbours in A, we need to find its k-dimensional vector d, and then we use it to calculate the weights for the information from the neighbours. The closer the neighbours are, the more weight their neighbours sum up to. The categorical label was transferred from A to B using one-hot encoding, which represented the label and label vectors corresponding to the k neighbours in A. The probability of the query cell is represented by the resulting vectors (bfL_rmqrmrrmy). The final assignment uses the category with the maximum probability.
In QC step 3, the experiments with fewer than 20 neurons were excluded to ensure the statistical power of projection analysis, resulting in 39,461 cells from 519 experiments left. The brain cells were taken out of the dataset and the rest remained. The cell-type classification method is described in the next section.
In quality control (QC) step 1, the cells included in the analysis are required to have a median mCCC level of the experiment < 0.025; 500,000 < nonclonal reads < 10,000,000; and mCCC level < 0.05. In total, 56,843 cells from 703 experiments satisfied these requirements (Extended Data Fig. 2a,b.
Source: Brain-wide correspondence of neuronal epigenomics and distant projections
Injection of rAAV-retro-Cre onto INTACT Mice for Retrograde Neuronal Labelling Experiments
As described previously2, to label neurons projecting to regions of interest, injections of rAAV-retro-Cre (produced by Salk Vector Core or Vigene, 2 × 1012 to 1 × 1013 viral genomes per millilitre, produced with capsid from Addgene plasmid No. 81070 packaging pAAV-EF1a-Cre from Addgene plasmid No. 55636) were made into both hemispheres of the INTACT mice. In summary, animals were anaesthetized with either ketamine–xylazine or isoflurane and placed in a stereotaxic frame. Pressure injections of 0.05 to 0.4 μl of AAV per injection site were made using glass micropipettes (tip diameters about 10–30 μm) targeted to stereotaxic coordinates corresponding to MOp, SSp, ACA, AUDp, RSP, PTLp, VISp, HPF, MOB, STR, PAL, TH, SC, VTA + substantia nigra, P, MY and CBX. The av was injected using iontophoresis to ensure confinedviral infection of PFC, ENT, PIR, AMY, HY and CBN. The glass pipettes used for iontophoretic injections had a tip diameter of about 10m. For most of the desired targets, injections were made at different depths and/or at different anterior–posterior orlateral coordinates. The Supplementary Table 1 has injection coordinates and conditions listed. At least two male and two female mice were injected for each desired target. A sample size calculation was not carried out. Minimum reproducibility was determined to be achieved using two mice of the same sex. Animals were randomly selected to be injected into the brain.
All experimental procedures using live animals were approved by the committee. A C57BL/6J background maintained the knock-in mouse line, R26R-CAG-loxp-stop-loxp-Sun1-sfGFP-Myc. Adult male and female INTACT mice were used for the retrograde labelling experiments. Animals were housed in an Association for Assessment and Accreditation of Laboratory Animal Care-accredited facility at the Salk Institute. There was a 12 h light and a 12 h dark cycle. Guide for the care and use of laboratory animals requires that temperature be monitored and adjusted. Humidity was not controlled but monitored. The fresh air coming in is the same as the ambient air outside, that’s why the humidity is the same. The humidity in San Diego is higher than the rest of the country. Animals were 35–54 days old at the time of surgery for viral vector injections, were killed 13–17 days later, and were 50–70 days old on the day of dissection. The wild type mice were used for MERFISH experiments.
Clustering snRNA-seq cells for GWAS with MAGMA v.1.10: a comparative study using a comparison of human and mouse gene sets
To determine which of our snRNA-seq cell types was enriched for specific GWAS traits, we used scDRS (v.1.0.2)50 with default settings. scDRS computes disease association scores and considers the distribution of control genes to identify cells associated with the disease.
We used MAGMA v.1.10 (ref. 101) to map single-nucleotide polymorphisms to genes (GRCh37 genome build from the 1000 Genomes Project) using an annotation window of 10 kb. The MAGMA y score is calculated by using the annotations and GWAS summary statistics to find out which genes are associated with which trait. Human genes were converted to their mouse orthologs using a homology database from Mouse Genome Informatics (MGI). The top MAGMA Z scores were weighted to pick the disease genes used in scDRS. Many of the traits we tested for enrichment had previously computed MAGMA z scores50, so those scores were used instead (after applying MGI gene ortholog conversion).
We used a ranked gene list and acurated transcription factor genes to identify the genes that were enriched for telencephalic excitatory or inhibitory populations. First, we ranked genes from our telencephalic excitatory cells by their average correlation with Fos compared with a background ranking of average telencephalic inhibitory Fos correlations. The telencephalic cells’genes were ranked in reverse order. We built a gene set of transcription factors by combining enrichR99 databases from ARCHS4, ENCODE and TRRUST. We subsetted for human transcription factors that showed up in at least two databases and had at least ten unique targets in each of those databases. The last part of the gene set had human transcription factors with targets in any one of the two databases. We used the R package fgsea v.1.20.0 to conduct the enrichment analysis, which was run against a background of all the genes shown in our pseudocell data. FDR was corrected using a positive one-tailed test.
We performed ward to further define our candidate ARGs. The clustering is done based on the correlations in the brain regions. We cut the dendrogram at a height that divided our ARGs into seven clusters. To assess the overlap between our ARG clusters and the ARGs reported in Tyssowski et al.42, we computed a Fisher’s exact test between two given gene sets using the R package GeneOverlap v.1.30.0 (ref. 98). P values were Bonferroni corrected for multiple hypothesis testing in each gene cluster.
The expression of pseudocell level genes was normalized using a log2transformed count per million. We further normalized the expression of each gene to have a mean expression of zero and a standard deviation of one. Normalized pseudocell counts were used for downstream analysis.
To generate our pseudocells, we first performed dimensionality reduction at the single-cell level. Single cells were divided into 27 groups, consisting of glial cell classes and neuronal populations further divided by neurotransmitter usage. The genes that were selected in each cell group had to be highly variable in a certain number of mouse donors so that we could scale them by batches. We used the scaled expression data to do principal component analysis on both glia and neurons. Next, we constructed pseudocells by grouping single cells within each cell type. Cells were assigned to pseudocells if they had the same size as the cell type.
Using scOnline, we aggregated our snRNA-seq expression data into pseudocells: aggregations of cells with similar gene expression profiles. The pseudocell resolution eliminates the technical variation issues of single cell transcriptomic data, such as low capture rate from dropouts and pseudoreplication through averaging expression of similar cells, while avoiding issues of pseudobulk approaches.
To quantify the uncertainty, we calculated the 95% confidence interval for the corresponding binomial distribution using the exact method of binconf function in the Hmisc R package92. For plotting clarity, regions with fewer than five total inhibitory and excitatory cells were excluded.
All cell types were assigned a NPR identity if the percentage of cells with non-zero NPR expression was greater than or equal to 0.2 and the average expression was greater than or equal to 500 counts per cell.
Each cell type was assigned to an NP ligand identity if (1) the percentage of its cells with non-zero expression of the NP was greater than or equal to 0.3 and (2) the average expression of the NP was greater than or equal to 0.5 counts per cell. We observed that the expression of four NPs showed greater contamination across other cell types: OXT, AVP, PMCH and AGRP. For these NPs, the percentage of cells with non-zero expression was required to be greater than or equal to 0.8 and the average expression to be greater than or equal to five counts per cell.
We looked at the top expressing transporters as well as the neurotransmitters of the 166 cells that did not meet the conditions.
Source: The molecular cytoarchitecture of the adult mouse brain
Cluster heterogeneity in cerebellum: Identifying the size of the universe set using a mixed integer linear programming model and CPLEX solvers
We framed the question as a set covering problem, so that we could find the minimally sized gene lists that allowed us to distinguish one cell type from the others. In the set cover problem, we find the smallest subfamily of a family of sets that can still cover all the elements in the universe set. The JuMP domain-specific modelling language in Julia can be used to define this as a mixed integer linear programming model. 33,89). We used the IBM ILOG CPLEX commercial solvers v.22.1.0.0 and the HiGHS open-source solver. Supplementary Methods uses a mixed integer linear programming model derivation and CPLEX solver parameters.
To generate the neighbourhood ridge plots in Fig. 2c, we first identified the interneuron and projection metaclusters for the isocortex, striatum and cerebellum, detailed in Supplementary Table 13. Supplementary Table 5 shows the cell types within each metacluster.
To generate the force-directed graph of regional cell type similarity, as in Fig. 2b, we weighted each pair of DeepCCF regions with the weighted Jaccard similarity metric. We then used the R package qgraph v.1.9 to generate a force-directed graph.
We used minimum cell types required to cover 98% of the beads in a study to assess cluster heterogeneity. We computed the number of beads based on the order in which each cell type was sorted. Next, we determined the number of cell types necessary for the running sum of beads to reach 95% of the total mapped beads.
Descendants were aggregated from more distant ancestors based on the index neuronal cell type. We continued aggregating until the number of cell types in the neighbourhood would surpass 100 or for neurons, if the next set of cell types was more than 60% non-neuronal.
The genes and cell types were first rearranged using the default permuting method. The cell types were then reordered to comply with the cell type dendrogram structure using a dynamic programming tree-crossing minimization optimization88.
We maximized the leaf sequence by changing the order of the children of the internal nodes in the tree. We did so by iteratively permuting the columns and rows of a normalized cell type by gene matrix so that the elements are grouped around the diagonal. Tbr1, Fezf2, Dlxes1, Lhx6, Foxg1, Neurod6, Lhx7, Sim1, Lmx1a, Lhx9 and Phox2b were chosen.
RCTD in doublet mode models how well explicit pairs of cell types match a bead’s expression. For computational efficiency, RCTD prefilters which cell type pairs are considered per bead. However, we found that larger cell type references with many similar cell types led to overly sparse prefiltering, which impeded our ability to confidently map fine-grained cell types. To balance this sparsity and control the potential overfitting of the pre-filtering stage we added an additional ridge regression term to RCTD, which allowed us to control the relative sparsity. Our modified prefiltering stage used a heuristic to detect a subset of potential cell types for each bead by using RCTD’s full mode with two ridge strength parameters (0.01, 0.001), as well as mapping each cell type individually.
We changed RCTD scores so that they aid in mapping large references with many similar clusters. We didn’t use the result of the single cell type pair that fit best, but we identified the cell type pairs that scored similar to the best- scoring pair. Then, we collated the frequency of each cell type occurring in these well-fitting pairs and divided by the total occurrences of all the cell types to make a confidence score. In our paper, we used a maximum score of 5 to set a threshold for a confident mapping.
We took out 10 cell types we thought were most likely to be associated with the bead, because they were explicit cell type pairs that RCTD used for doublet mode. We only used one cell type from the top 10 list and a different cell type from the rest of the pre-filtered list to model how well these cell types mapped to a bead. The number of cell types considered for the cerebellum and striatum was sufficiently low that we were able to run the program.
We changed the quadratic programming optimizer of RCTD to use OSQP81, which scales better for the larger matrices resulting from larger sets of cell types to be mapped. We also rewrote the inner loops of the most time-intensive functions (choose_sigma_c and fitPixels) with Rcpp82 for efficiency. We were able to parallelism to thousands of cores using cloud computing services with the help of Hail Batch and GNU Parallel 85.
Source: The molecular cytoarchitecture of the adult mouse brain
Building a quality network for immune cell populations using SCOPIT, Seurat clustering, and OpenTSNE v.1.1.4
We identified 16 cell classes in the data, but 6 of them weren’t included in the majority of our analyses. Most of these excluded clusters are classified as immune cell types and are mentioned in the following figure and tables: Extended Data Fig. Supplementary Tables 2 and 3 are included. In addition, we mapped many immune cell populations.
We used the R package SCOPIT v.1.1.4 (ref. 80) to estimate the sequencing saturation of our dataset. Under the prospective sequencing model, SCOPIT calculates the multinomial probability of sequencing enough cells, n, above some success probability, p, in a population containing k rare cell types of size N cells, from which we want to sample at least c cells in each cell type:
Our next step was to identify and remove low-quality cells from the dataset. By simultaneously considering multiple quality metrics, our network-based approach has increased power to identify low-quality cells while circumventing the issues related to setting hard thresholds on multiple quality metrics. To construct the quality network, we considered the following cell-level metrics: (1) per cent expression of genes involved in oxidative phosphorylation; (2) per cent expression of mitochondrial genes; (3) per cent expression of genes encoding ribosomal proteins; (4) per cent expression of IEG expression; (5) per cent expression explained by the 50 highest expressing genes; (6) per cent expression of long non-coding RNAs; (7) number of unique genes log2 transformed); and (8) number of unique UMIs (log2 transformed). Given their inherently distinct distributions of quality metrics, we separately constructed quality networks for neurons and glial cells. The quality network was built using shared nearest neighbour and Leiden clustering of the Seurat v.4.2.0. We had a strategy to remove any cluster from the quality network with morelier distribution of quality metric profiles. A distribution of quality metric was considered an outlier if its median was above 85% of cells in the quality network. We further removed any remaining clusters with fewer than 15 cells.
For high-dimensional visualization. 1a, we first subsampled each of the clusters to a maximum of 2,000 nuclei. The first 250 principal parts of our cells were calculated using the Scanpy package. We then ran OpenTSNE v.1.0.0 (ref. 78) on the principal component space to generate a t-SNE that optimizes both local and global structure using an exaggeration factor of four and a perplexity of 350.
If the next level of clustering resulted in a set of differential clusters that passed this test, there was only one exception; this was a situation when the first round of clustering split cells on a continuous difference in expression. We retained these clusters for further subclustering as they may contain additional structure.
We looked at each leaf and its sibling leaves to test for differential markers. We used a U-test to see if any genes are differentially expressed. As an additional filter, we required that a gene be observed in less than 10% of the lower population and observed at a rate at least 20% higher in the higher population to ensure that there is a discrete difference in expression between the two populations. Every cluster must have at least three marker genes distinguishing it from its neighbours as well as three marker genes in the other direction. All leaves were merged if the cluster failed the test.
If the resolution sweep concluded at the highest resolution without ever finding multiple clusters, this is also indicative of a homogenous population, and clustering was considered completed.
There is not a resolution low enough to form a single cluster if the neighbour graph is not a single connected component. This would typically occur if there were very few variable genes, which is indicative of a homogenous cell population.
Once we computed the shared nearest neighbour graph, we used the Leiden algorithm to identify cell clusters using the Constant Potts Model for modularity77. This method is sensitive to a resolution parameter, which can be interpreted as a density threshold that separates intercluster and intracluster connections. To find a relevant resolution parameter automatically, we implemented a sweep strategy. We started with a very low-resolution value, which results in all cells in one cluster. We gradually increased the resolution until there were at least two clusters and the size ratio between the largest and second-largest cluster was at most 20, meaning that at least 5% of the cells are not in the largest cluster. A group of less than N cells was discarded, where the number was clustered in that round. This discarded set constituted roughly 1.6% of the total cells (100,280 of 5.9 million).
We constructed a shared nearest neighbour graph after selecting variable genes. First, we transformed the counts with the square-root function and then computed the k-nearest neighbour (kNN) graph using cosine distance and (k=50) (not including self-edges). From the kNN graph, we compute the shared neighbour graph, where the weight between a pair of cells is the Jaccard similarity over their neighbours:
In order to find genes that are observed at least 5% less than expected, we compared the expected value with observed percentage of non-zero counts.
We analysed three genes with highly stereotyped and regional expression, Dsp, Ccn2 and Tmem212, which correspond to the CCF regions detailed in Supplementary Table 12.
The main regions of the CCF hierarchy were grouped according to their importance. For many of our analyses, we also grouped into ‘DeepCCF’ regions, detailed in Supplementary Table 4.
The 50 m resolution sections were aligned to the 50 m CCF by estimating three transformations. First, a three-dimensional diffeomorphism modelled any shape differences between our sample and the atlas brain. This transformation is modeled using the Large Deformation diffeomorphic Metric mapping framework. The third, a three-dimensional affine transformation was used to show any pose or scale differences between the sample and the atlas. Third, a two-dimensional rigid transformation (three degrees of freedom per slice) on each slice modelled positioning of samples onto microscopy slides.
Dissimilarity between the transformed atlas and our imaging data was quantified using an objective function we developed previously69,70, equal to the weighted sum of square error between the transformed atlas and our dataset, after transforming the contrast of the atlas to match the colour of our Nissl data at each slice. To transform contrasts, a third-order polynomial was estimated on each slice of the transformed atlas to best match the red, green and blue channels of our Nissl dataset (12 degrees of freedom per slice). During this process, outlier pixels (artifacts or missing tissue) are estimated using an expectation maximization algorithm, and the posterior probabilities that pixels are not outliers are used as weights in our weighted sum of square error.
For each puck we created a greyscale intensity image from the Slide-seq data by summing the UMI counts across all genes and then normalized it. We then performed the alignment of these images to the adjacent Nissl images in two steps. First, we transformed each Nissl image to an intermediate coordinate space using a manual rigid transformation. The purpose of this first transformation is to bring all the Nissl images to an upright orientation which made the second step easier. In the second step, we manually identified corresponding fiducial markers in the Nissl images and Slide-seq intensity images using the Slicer3D tool v.4.11 (ref. 66) along with the IGT fiducial registration extension67. We used fiducial markers to determine the parameters of the thin-plate interpolation where the bead positions were computed.
To match the bead barcode between reads the sequence was aligned to the reference and processed using the slide-seq tools.
Source: The molecular cytoarchitecture of the adult mouse brain
Nissl Images of the Brain Using the Olympus VS120 Numerical Aperture Objective and a pike 509c Camera
We acquired Nissl images on an Olympus VS120 microscope using a ×20, 0.75 numerical aperture objective. The images were taken with a pike 509c VC50 camera under autoexposure mode and a halogen lamp. The width and height of the images all had the same resolution of 0.3437 m. We acquired a total of 114 Nissl images, each from an adjacent section of the brain to a corresponding section that was processed using the Slide-seq pipeline. Ten were removed from the upper and anterior medullas of the 114 sections to make room for the CCF reference brain. Of the remaining 104 images, we removed an additional three sections because of the unsatisfactory quality of the corresponding Slide-seq puck data. The remaining 101 images comprise the final dataset that we use for all our analyses.
slight modifications were made to the slide-seq arrays. Larger diameter gaskets were used to generate the bead array. The sizes were chosen to help the different parts of the body. We used 2 2 digital binning on the collected data to facilitate image processing.
CellRanger v.5.0.1 used default settings for demultiplexes and aligned reads to a reference. The cells were removed with the help of CellBender v.3- alpha63.
Source: The molecular cytoarchitecture of the adult mouse brain
BICCN mouse-brain atlas: Anisoflurane injection in dissection tray of C57BL/6J mice for regional tissue dissections
At 56 days of age, C57BL/6J mice were anaesthetized by administration of isoflurane in a gas chamber flowing 3% isoflurane for 1 min. The negative tail pinch response was confirmed as a result of Anaesthesia. Animals were transported to a dissection tray, where they were put under anesthesia with a 3% isoflurane for the duration of the procedure. The heart was donated with an ice-Cold pH 7.4 HEPES buffer containing 120 mM. NaCl, 10 mM HEPES, 25 mM glucose, 75 mM sucrose, 7.5 mM MgCl2 and 2.5 mM KCl to remove blood from brain and other organs sampled. For use in regional tissue dissections, the brain was removed immediately; the meninges was peeled away from the entire brain surface, then frozen for 3 min in liquid nitrogen vapour and moved to −80 °C for long-term storage. For use in generation of the Slide-seq dataset through serial sectioning, the brains were removed immediately, blotted free of residual liquid, rinsed twice with OCT to assure good surface adhesion and then oriented carefully in plastic freezing cassettes filled with OCT. These cassettes were vibrated in a Branson sonic bath for 5 min at room temperature to remove air bubbles and adhere OCT well to the brain surface. The brain’s precise orientation in the x–y–z axes was then reset just before freezing over a bath of liquid nitrogen vapour. Frozen blocks were stored at −80 °C.
After arrival animals were allowed to acclimatize to their housing environment by living in a 12-h light–dark schedule followed by two weeks of 30– 50% humidity. All procedures involving animals at Massachusetts Institute of Technology were conducted in accordance with the US National Institutes of Health Guide for the Care and Use of Laboratory Animals under protocol number 1115-111-18 and approved by the Massachusetts Institute of Technology Committee on Animal Care. All procedures involving animals at the Broad Institute were done in accordance with a US National Institutes of Health guide for the care and use of laboratory animals.
The BICCN mouse-brain atlas is open to the public and is intended to serve as a reference for scientists studying brain disorders and brain evolution across species. It is not the only one of its kind. Several mega brain projects, each trying to make their own reference atlas or reference model, are under way around the world.
The BICCN was launched in January of this year and is a collaboration between 250 scientists at 45 institutions across three continents that is funded by the National Institutes of Health.
These include Japan’s Brain/MINDS project to map the marmoset (Callithrix jacchus) brain4, China’s Brain Project, focusing on macaque monkeys (Macaca spp.)5 and the Korea Brain Initiative, which aims to develop specialized brain maps for both mice and humans6.
Scientists at the European Union’s Human Brain Project (HBP), which was based in Geneva, Switzerland, and ended in September, have also created the Human Brain Atlas. This is available on the HBP’s open platform EBRAINS. The atlas uses post-mortem brain-imaging data and depicts the multilevel organization of the brain, from its cellular and molecular architecture to its functional modules and neural connections.
The Swiss Blue Brain Project, which will wrap up in 2024 after nearly 20 years, will also release a digital model of the mouse brain, based on imaging data, with detailed mapping of neurons and connectivity circuits.
Towards an Open Data Standard for Cell-Clusters: The Challenge of Big Data Collectivity and Big Data Analyse
Each of these projects is important in its own right, but as they progress — some have been going more than ten years — there is a need for better communication between them. A number of the projects use technologies that are similar. It makes sense for the teams to liaise more closely, at the very least to begin a discusson on how to establish shared data standards, which they have not yet done.
At a minimum, the data, models and code need to be open. Even then, very large data sets such as these still pose a challenge to reproducibility. It is necessary to standardize the framework for data collection and analysis, which will eventually include definitions for different types of cell clusters.
Our study found that there’s statistically significant higher enrichment (P = 0.004) of chromatin interaction signals at the corresponding-specific cCRE-gene pair anchors, compared with non-corresponding pair anchors. This suggests that cCRE-gene pairs are more likely to interact in cell types in which the cCREs are active. We used snRNA-seq cells for GWAS with MAGMA v.1.10 to compare human and mouse gene sets.