There is evidence of human influence on snow loss in the Northern Hemisphere
by admin
Snowfall and water availability off the Northern Hemisphere – an in-situ comparison with snowpack data from the European Center for Medium Range Weather Forecasting
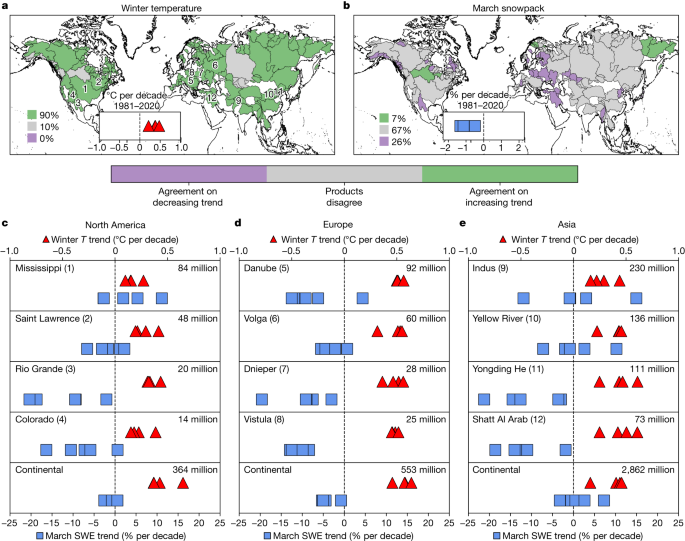
The researchers only saw a small amount of snow loss in parts of the Northern Hemisphere that have colder winters. Parts of Alaska, Canada, and Central Asia even experienced increased snowpack. Eventually, though, if the planet keeps heating up, even those places could fall off the snow-loss cliff.
“Where the majority of people live and where the majority of people put increasingly competitive uses on water availability, particularly from snow — they live in places that are at or on this snow-loss cliff,” said Justin Mankin, an associate professor of geography at Dartmouth and senior author of the new research paper.
After a basin falls off a cliff, it isn’t about managing a short-term emergency until the next big snow. They will adapt to permanent changes in water availability.
The European Center for Medium-Range Weather Forecasting is a component of our ensemble of SWE observations. Products with a submonthly temporal resolution are averaged across all available March values. We can benchmark our results in March if we take in situ measurement during the month of maximum snow mass in the Northern Hemisphere. Because the satellite remote-sensing-based Snow-CCI product is masked over mountainous terrain, we follow the approach of ref. 20 and fill SWE values in mountainous cells with the mean value from the other four data sources. For non-mountainous grid cells, we use the unaltered Snow-CCI data. The Snowpack Telemetry Network in the western USA50 and the Canadian historical Snow Water Equivalent dataset are both seh data we use as part of our data set. Only in situ observations with records for at least 35 years between 1981 and 2020 are retained, resulting in a set of 550 from SNOTEL, 341 from CanSWE and 2,119 from NH-SWE.
Alex Gottlieb, the first author of the study and a PhD student at Dartmouth said they were able to identify a clear fingerprints of emissions. They could clearly see that pollution from fossil fuels had a negative impact on snow trends in the Northern Hemisphere.
It’s been hard to make this connection until now because global warming leads to both higher temperatures and more precipitation, which can counteract each other. You might have a warmer average temperature, but heavier snow in a storm.
The new research shows a surprising relationship between the temperature and snow mass, as well as having complex ramifications, writes a research professor in an accompanying article.
The University of California, Los Angeles Institute lead for climate science says the study highlights the vulnerability of the region because of it’s dependence on both the Colorado River Basin and Sierra Nevada.
We calculate the temperature response to anthropogenic forcing as the difference between the 30-year rolling mean average temperature for each month in the HIST and HIST-NAT runs. The forced response is calculated from the difference between the 30 year rolling mean monthly precipitation in HIST and HIST-NAT. We want to limit the model biases in temperature and precipitation by differencing the experiments from the same model. Systematic biases in the model-simulated trends (for example, too rapid warming or wetting), however, could potentially lead to over- or under-estimating the forced response. The model biases in the 1981– 2020 trends in winter temperature and precipitation are evaluated using the CMIP6 HIST ensemble mean and the mean of the observational products for each quantity. To find out if the observed trends are consistent, we ask them if they fall within the range of forcing plus internal variability of the CMIP6 HIST trends. Climate models capture realistic climate trends, and only 1% of grid cells fall outside this range for temperature.
Average cold season temperature in that same unit is March swei, which is the month of March in water year Y and Ty, which is the month of Ty. We run this regression at each in situ location, for all 20 combinations of gridded SWE and temperature products, for all 12 climate models (using the HIST simulations), and for all 120 basin-scale reconstructions. We use 5 temperature window to calculate the average and standard deviation of the coefficients for different types of data, such as observations, climate models and basin-scale reconstructions. 4a. Both data and parametric uncertainty are included in the uncertainty estimate.
All estimates of basin population are calculated using the 2020 values from the 15 arcmin Gridded Population of the World, Version 4 (GPWv4) dataset from NASA’s Socioeconomic Data and Applications Center60.
Modeling the Spatiotemporal Patterns of Sudden Water Events with a Full Panel of Grid Cell Observations and HIST Simulations
The correlation of the map of trends from observational products and the multimodel mean map from the HIST simulations is used to quantify the similarity between the observed patterns of SWE trends and model-estimated response to forcing. The mean trend of the stations within each grid cell is used for this analysis as well as the gridded observations and climate models. If the correlation between the observations and HIST simulations is greater than most of the correlation between the HIST and PIC simulations, then we can reject the argument that the observed historical pattern could have arisen from natural variability alone, and claim that a response to historical forcing is present in the observed pattern The null hypothesis can’t be rejected because it isn’t unlikely that the observed pattern is due to natural radiative forcing. Combined, these two lines of evidence strongly indicate that anthropogenic forcing is causing the observed patterns of SWE trends.
where SWEy,i is average March SWE in water year ( October–September) y at grid cell i, f is the random forest model, Ty,m,i is the average temperature in month m of water year y and grid cell i, and Py,m,i is the total precipitation in month m of water year y and grid cell i. We fit the model using the full spatiotemporal panel of 0.5° × 0.5° gridded data (that is, all grid-cell years from 1981 to 2020), then aggregate the predicted gridded values to the river-basin scale. There are two main advantages to training a single model on the full panel of data, compared to training multiple models on more local data. First is that the out-of-sample prediction skill of the full panel model is significantly higher in many highly populated mid-latitude basins of the western USA, western Europe and High Mountain Asia; local models are more skilful in fewer than 20% of basins, concentrated in sparsely populated high-latitude basins where the skill of the full panel model is already high (Extended Data Fig. 3). Second, training a single model on data from the entire hemisphere provides greater statistical stability of projections made with large perturbations to the input variables, such as adding an end-of-century climate change signal (Extended Data Fig. 8), which could exceed the support of local historical observations as records fall at an increasing rate65,66.
As an additional test of model skill, we use a model trained on observational products only to forecast fully out of sample March swer at 2,46 in situ sites from the SNOTEL, CanSWE and NH-SWE datasets. Our reconstructions can represent the interannual variability within in situ SWE with a median R2 of 0.59 and an estimate of 22%. The reconstruction model predictions are able to capture the long-term SWE trends at the in situ sites and have a pattern correlation of 0.72. We have confirmed that there are no systematic trends in time of the bias of our reconstructions against in situ observations.
The uncertainty from SWE observations, TP, M, and I are the three components that make up the uncertainty from model structure. To determine which sources are the largest contributors to uncertainty in each basin, we consider the fractional uncertainty of each. This uncertainty is reported in supplementary fig. For each source, we hatch out basins where the magnitude of uncertainty is insufficient to change the sign of the ensemble mean estimate of the forced SWE trend (that is, the signal-to-noise ratio is >1).
SWE change calculations use equation(4), but substituting the estimates from the future for historical values of precipitation and temperature.
The model biases in 1981–1981 are evaluated by evaluating the CMIP6 HIST ensemble mean and the mean of the products for each quantity. We run this regression at each in situ location, for all 20 combinations of gridded SWE and temperature products, for all 12 climate models (using the HIST simulations), and for all 120 basin-scale reconstructions.